Country Jazz Lesson: John Scofield’s Cover of "Mama Tried" Part 2

Last time, we looked at the melody and form to John Scofield’s instrumental cover of “Mama Tried," the popular country tune written by Merle Haggard, which Scofield recorded for his Grammy Award-winning 2016 album Country for Old Men. 

In this conclusion to our two-part lesson, we’ll focus on highlights from Scofield’s improvised solo and discuss how he used jazz vocabulary to imply sophisticated harmonic movement over the basic underlying chord progression. 

As stated in part 1, Scofield played his arrangement in standard tuning and in the concert key of Eb. He also used a capo at the 1st fret. For purposes of this lesson, we’ll forego the use of a capo and tune our guitars down a half step, to Eb standard (low to high: Eb, Ab, Db, Gb, Bb, Eb), and think “key of E.” 

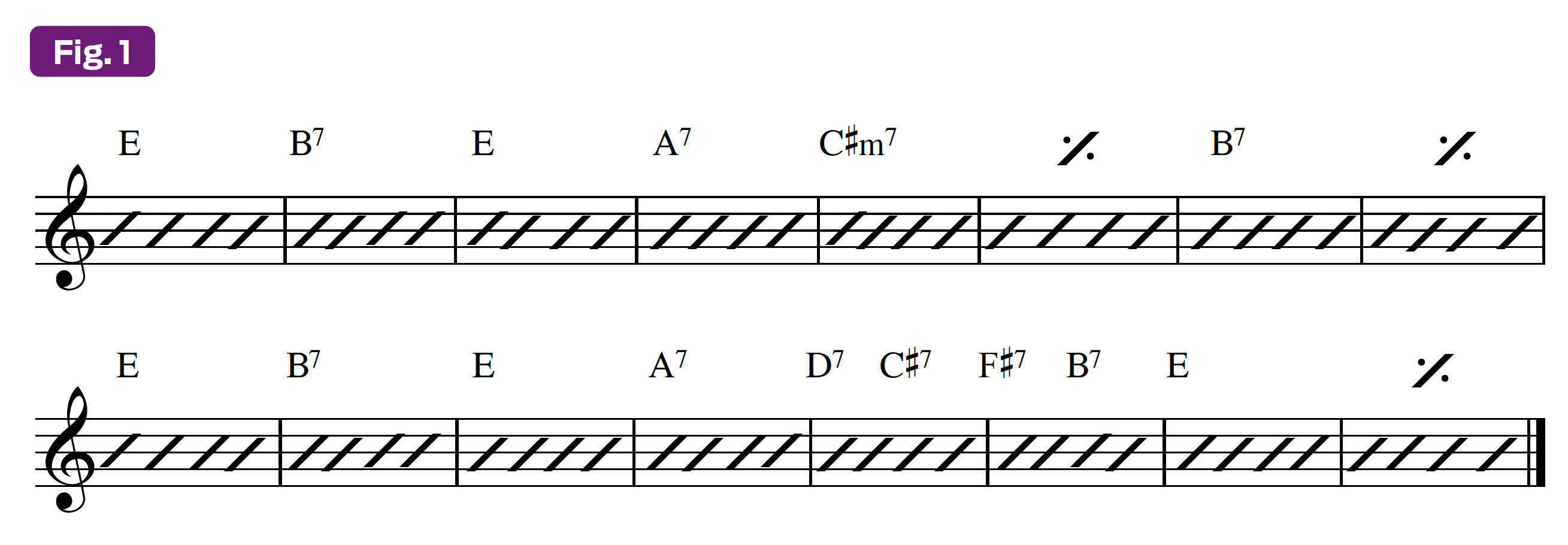
The solo is played over the repeating 16-bar chord progression that functions as the verse in the main melody section (see Figure 1). Although the tune is built around basic chords, the single-note lines that Scofield plays imply more complex harmonic moves that are usually associated with jazz and bebop. 

In the following examples, we’ll discuss a few concepts Scofield used and how they were tastefully applied to this simple form. 

If you’ve ever played a 12-bar blues, you’re familiar with the term turnaround. This refers to the last two bars of the repeating form, where the chord progression comes to a conclusion by setting up a compelling return to the beginning of the form.

You can also find various turnarounds in other chord progressions and forms. For example, in “Mama Tried,” the solo section is a repeating 16-bar form, for which the last four bars function as the turnaround.

All the turnaround examples we will examine in this lesson are based on the chord progression D7 - C#7 - F#7 - B7, which cycles back to the I chord, E. It’s important to note that the lines John played over the turnaround often imply added harmonic extensions on top of the basic chord structure, which is why I have included the names of the “implied” chords above the staff in each of the following examples.

Try using a looper pedal to record the implied chords, or have someone accompany you, so that you can hear how the single-note lines effectively describe the more complex implied harmony. 

If you’re playing with a bass player and no other chord instrument, he or she can play the root notes to the basic country changes and you can play all of these fancy licks over top without any problems, and it will sound cool.

However, if you do have a chord instrument playing with you, the fancy stuff might make more sense to your ears if the person accompanying you reinforces the implied chord changes. I recommend experimenting with both approaches and comparing the difference between them.

The first turnaround we’ll examine is shown in Example 6 and occurs in the last four bars of Scofield’s first solo chorus (0:55–1:01) The first half of the line cycles through the progression D13 - C#7 - F#7b9 - B7. This is basically the same progression as D7 - C#7 - F#7 - B7 but with some implied harmonic extensions on the D7 and F#7 chords. If you ever have to solo over a fast tune with chords that change at the rate of two to a bar, you can simplify things by addressing only the second chord in each bar.

For instance, in the first bar of this turnaround, we have D13 to C#7, which can be simplified to C#7, in terms of what chord to target. And in the bar that follows, we have F#7b9 to B7, which likewise can be reduced to one bar of B7.

In other words, we have simplified the solo changes to one bar of C#7 followed by a bar of B7. On C#7, John plays notes from the C# Mixolydian mode (C#, D#, E#, F#, G#, A#, B) with the passing tones A (the b6) and E (the b3) added. The A falls on an upbeat of beat 1 and serves as a lead-in note, whereas the E falls on the downbeat of beat 3 and resolves to the major 3rd of the C#7 chord, E# (written here as F). 

Scofield takes a similar approach with the B7 chord that follows in the second bar, this time using notes from B Mixolydian (B, C#, D#, E, F#, G#, A) with the passing tones G (the b6), and D (the b3), where the G is a lead-in note and the D resolves to D#, the major 3rd of B7.

Notice in the last two bars of this example where the basic changes suggest an E chord while the implied changes indicate B7. This is because this line implies a continuation of the B7 chord from the previous bar, which creates a delayed resolution to the E chord at the end of the phrase.

Example 7 illustrates what John plays over the four-bar turnaround that occurs at the end of his second solo chorus (1:13-1:18). Like the previous example, it implies some different extensions to the basic turnaround chords. The first half of the line, played over the basic turnaround D7 - C#7 - F#7 - B7, implies extensions that suggest D7#11 - C#13 - F#9 - B13.

Just like in the previous example, we can reduce the two chords in each bar to one for a simpler analysis. In the first bar of this turnaround, we have D7#11 to C#13, which can be simplified to C#13 and in the measure that follows, we have F#9 to B13, which likewise can be approached as if it were one bar of B13.

In other words, we have simplified the solo changes to one bar of C#13 followed by a bar of B13. One way to explain this line is to say he’s playing C# Mixolydian notes with an E passing tone over C#13 and then B Mixolydian with a D passing tone over B13. 

The next two bars of Example 7 are played over the changes G#m7 - C#7 - F#m7 - B9. This presents another opportunity to reduce two chords in a bar to one. In this case, G#m7 to C#7 can be reduced to C#7, and F#m7 to B9 can be reduced to B9.

Once the chord progression is simplified in this way, it becomes easier to see that this line contains notes from C# Mixolydian for a bar over C#7, followed by B Mixolydian on the bar of B9.  

The third turnaround phrase we’ll look at utilizes a different approach than the previous two. The lick shown in Example 8 occurs at the end of John’s fourth solo chorus (1:48-1:51) and implies the progression G#m7 - C#13 - C#7/E# - B9.

Notice that the turnaround progression is mostly the same except for the C#/E#. If you listen carefully to the recording, you’ll hear that there is a strong F (E#) in the bass, which suggests that this chord is not the expected F#7 but rather a C#7 with its 3rd in the bass.

All of the melody notes used in the line are in the key of E, with the exception of the C natural in the first bar and F natural in bar 2. The C natural could be considered either a chromatic passing tone or the b7 on the D7 chord in the cycle.

The F natural (E#) functions as a targeted major 3rd of C#7 that’s approached by two chromatic pitches below it. Even though these passing notes are not diatonic to the key of E, they can be justified in that they directly correspond to the chords that are played in the cycle. 

When soloing over chord changes, an effective improvisational strategy is to aim for specific chord tones to land on in advance, in order to give your lines a strong sense of direction.

This can be done by using chord tones for the target notes and placing them on the strong downbeats rather than the weak upbeats. In the next featured excerpt from John’s solo, we have a long phrase that uses chord tones as target notes on the downbeats in an ascending line in the key of E.

Here, the main target notes are E on the E major chord, F# on the B7, B on the next E major and C# on the A major. If you take a second to play these target tones as basic whole notes over each chord, you can really hear how the line has a simple, almost nursery rhyme-like quality (see Example 9a).

The line comes to life in Example 9b (1:00-1:07), where Scofield adds notes around the target tones that “decorate” them, resulting in a sophisticated lick with a target line on top and a decoration line on the bottom. The last part of this example concludes with a call-and-response-type line in E major over the last four bars.

Our next example demonstrates Scofield’s use of the half-whole diminished scale, which, as its name indicates, follows a formula of alternating half steps and whole steps. 

Among jazz musicians, this is a favorite scale to play over dominant 7th chords, and it has been used extensively by many of the greats, such as John Coltrane, Allan Holdsworth and many others.

In Example 10a (1:07-1:09), we see a short, two-bar lick that Scofield plays over the V (five) chord, B7, which effectively describes a B7#9b9 chord sound via the use of notes from the B half-whole diminished scale  (B, C, D, D#, F, F#, G#, A).

Notice how the scale includes the foundational chord tones of B7 (B, D#, F# and A), as well as the extensions b9 and #9 (C and D, respectively). This short idea makes for a colorful and interesting phrase, and it’s an example of one of John’s signature moves that he has used in other solos.

Experiment by altering the rhythm, or try doubling the length of the phrase by repeating it up an octave, as indicated in Example 10b. The altered scale is another popular scale that can add tension to your lines when playing on dominant chords.

Also known as the diminished whole-tone scale and the super-Locrian mode, the altered scale is the 7th mode of the melodic minor scale and includes the altered chordal tensions b9, b5, #9 and #5. 

In Example 11, we have an idea from bars 7 and 8 of John’s third solo chorus (1:24-1:26), where he uses the B altered scale (B, C, D, Eb, F, G, A) over a B7#5 chord.

Notice how most of this lick consists of simply playing down the scale beginning on Eb/D# and descending until landing on, F – Eb, D, C, B, A, G, F. The tension within this lick is particularly effective due to the fact that it is placed at the end of the phrase, where the harmony leads back to E major.

This is a good place to experiment using altered sounds because the altered extensions feel less out of place where tension is desired. We recommend recording the chords and playing this line over them in order to get a feel for the way the harmony resolves from B7#5 to E. 

In Example 12, we have another line based on the altered scale, which John played in bars 7 and 8 of his fifth solo chorus (1:58–2:01). Like the previous example, this lick uses the B altered scale and offers a good musical demonstration of a descending line that outlines a B7 altered-dominant chord resolving to E.

When experimenting with this scale, keep in mind that the altered sound is quite dissonant. As such, it may require restraint and discretion in order for it to be most effective.  Many jazz improvisers deliberately manipulate specific chromatic passing tones in their lines to create bebop sounds.

Take a look at Example 13, which begins at the top of Scofield’s fourth solo chorus (1:34-1:37) and includes notes from the E major scale (E, F#, G#, A, B, C#, D#), with b6 and b5 passing tones, respectively C and Bb (notated as A#). The chromaticism that is created by adding these notes allows for what is known as enclosure in bebop music.

In this case, the target note, B, is first approached by C#, C natural and Bb. Instead of just playing the note B, we can decorate it, or “dance around it” by approaching it with neighboring chromatic pitches.

One could say that these notes “enclose” the target note since the pitches move chromatically around the destination note, both above and below it, before landing on it. This type of deliberate chromaticism is commonly found in the bebop vocabulary and can be heard in many jazz melodies and solos. 

Exploring various interval combinations in your single-note lines can be a great way to help you break away from old patterns and create new sounds. 

The first half of the lick in Example 14 begins at the 5th bar of the fourth solo chorus (1:39-1:45) and is a cool example of interval combinations that yield a fresh sound and an interesting melodic contour.

The first part of this example is played over C#m and begins with a minor 2nd interval (B to C), followed by a tritone (C to F#), a 4th (F# to B), a minor 3rd (B to G#) and two more 4ths (G# to C# to F#). Notice how the frequent use of ascending 4ths creates a spacey, “open” sound, which gives us a different result than your typical minor pentatonic blues lick. 

The second half of this line is played over B7 and is a great example of a bebop line that resolves from the V7 chord to the I (B7 to E) at the end of a phrase. Most of the notes Scofield plays over B7 here are from B Mixolydian, but there are also a couple of additional passing tones.

The first occurs in bar 4, where he slides up to a G natural on beat 1, which creates a B7#5 sound. The second passing tone is the A# that’s added to the line midway through bar 4. Since the line is played over B7, this chromatic passing note may be considered to be part of the B bebop scale, which, ascending, is spelled B, C#, D#, E, F#, G#, A, A#, and is the same as B Mixoloydian but with an added A#. 

We hope you enjoyed these lessons. We highly recommend having a listen to both the Merle Haggard and John Scofield versions of “Mama Tried” for context, inspiration and enjoyment. Remember to practice improvising with a looper or another guitarist and begin by soloing on the basic changes.

Once you have a feel for the tune, try improvising on the implied changes and plug in some of the examples presented in this lesson. As you become more familiar with these ideas, see if you can create some of your own variations that can be applied to other progressions.